A few months ago, I prepared this post but didn't feel ready to publish it. It raised more questions than it answered, so I wanted to have a little more background about it. Hopeless wish! There's so much about angles that I don't fully understand. With pi-day approaching, I'm also looking for some inspiration about circles and angles, so I thought publishing might get me in the direction...
I really became aware of the difficulty to divide an angle into three equal angles (a.k.a. angle trisection) some three years ago. It's bloody hard to find general procedures to divide precisely a circular arc into three equal arcs. There are some tricks that are well documented on the web, but you won’t find a simple geometric procedure using only a compass and an unmarked ruler. It has even been "proven" impossible. We only know of some "cheating" tricks like using a marked ruler (for Archimedes' trisection), origami or mechanical tools that will allow you to trisect precisely an angle. And there is an equilateral triangle that appears "by miracle" when you trisect all angles of a triangle, a result found by mathematician Frank Morley (because he himself tried to better understand or crack that impossibility?). So the angle trisection really became to intrigue me and I progressively dug into it.

One of the questions that has obsessed me is : How do we characterize an “Angle”? I’ve already written a post on that question, pointing out the utility of the chord subtending the circular arc of a circle of unit diameter. The measure of this chord is what we call the sine of the subtended angle. It characterizes the angle and it greatly facilitates our way to count angles, for example by progressing stepwise with chords in a circle.
Roughly speaking there are two ways to manipulate angles with circles. Either you use central angles, meaning that you fix the vertex and you radiate towards the circle in order to subtend an arc, or you use inscribed angles, meaning that you put the vertex of the angle on the circle. Figure 1 shows the equivalence between both methods. The central angle of a subtended arc in a circle of radius 1 is equal to the same angle when it is inscribed in a circle of diameter 1. This equivalence between central and inscribed angles is another way of stating that the measure of a central angle is exactly twice the measure of the inscribed angle, the factor 2 expressing the ratio between diameter and radius.
Figure 2 and 3 illustrate some advantages of inscribed angles. You can put the vertex anywhere on the circle: if the subtended circular arc (or its chord) remains constant in length, the angle remains the same. For the case when the vertex is located between the two endpoints of the subtended arc, you have to add the parts at each side of the vertex.
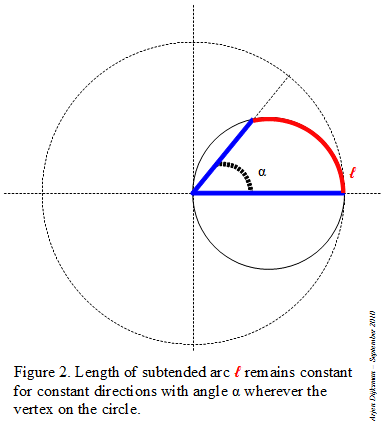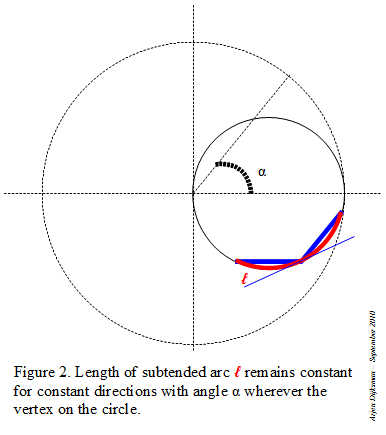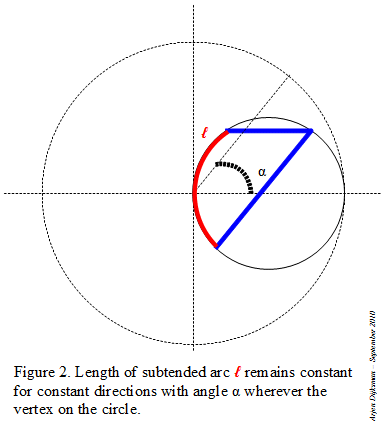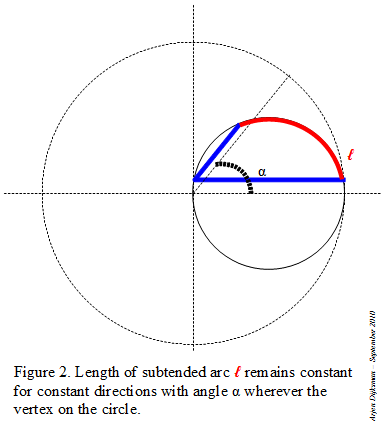 |

This flexibility of inscribed angles opens possibilities that remain hidden for central angles. If you combine different circles at intersections with straight lines, you’re simply calculating with angles. Figure 4 illustrates an alternative way to count angles. Starting with an angle α inscribed in a circle of unit diameter, if we draw a unit circle symmetric to the chord of the subtended angle, we can read off an angle (

The interesting thing is that wherever we shift a unit circle in this setting, the opposite subtended arcs differ always by an angle amount α, as shown in Figure 5 (in fact the circle needn't be aligned on the axis). So this allows us to add or subtract any angle to another angle.




No comments:
Post a Comment