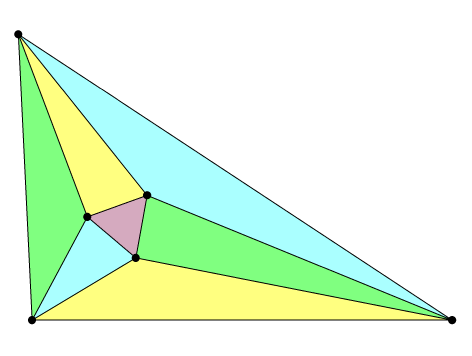
 |
| Morley equilateral triangle at the intersection of the trisectors (from Wikimedia Commons) |
Frank Morley was an excellent teacher and chess player (see some more about him at Pat'sBlog). If he had lived today, I like to think of him having his own blog communicating about his passion for math and chess, submitting his recreational problems. If he hadn't discovered the equilateral triangle at the intersection of trisectors, it's probable that this theorem would still be unknown. Trisection of angles is a controversial subject for research, especially among academia, where it is associated with suspicion of crankiness (see Underwood Dudley's book about trisectors). A pity... because trying to understand how to divide angles is a "natural" question, of which we shouldn't be ashamed, provided that we modestly take into account what has been found by other people.
All the proofs of Morley's theorem that I know of start with a result: an equilateral triangle or a triangle already drawn with its trisectors (see the different proofs referenced on the very complete French site Abracadabri or at the end of Alexander Bogolmony's Cut the Knot site). In this sense, they are backward proofs, which keeps some mystery about the physical origin of the equilateral triangle. I tried something different, a bit similar in spirit to my Archimedes tripling circle: How can we multiply an angle by 3, from which would result a Morley triangle embedded in a triangle of any shape? So here follows an alternative forward proof for Morley's theorem.
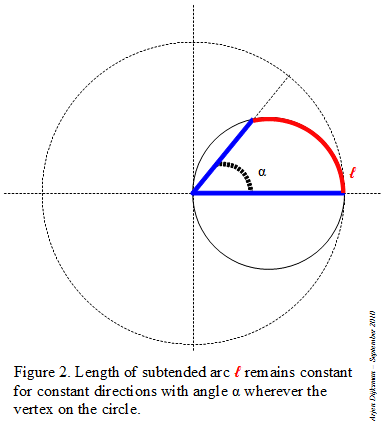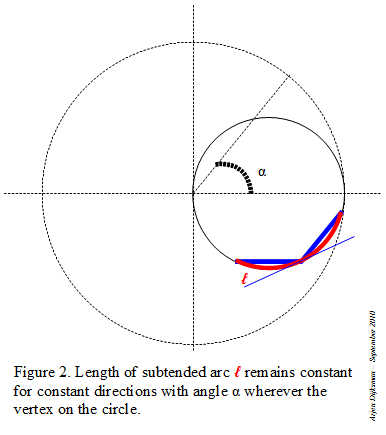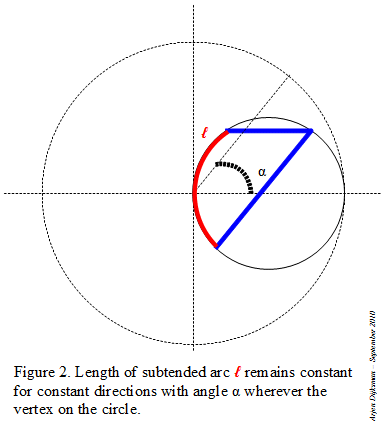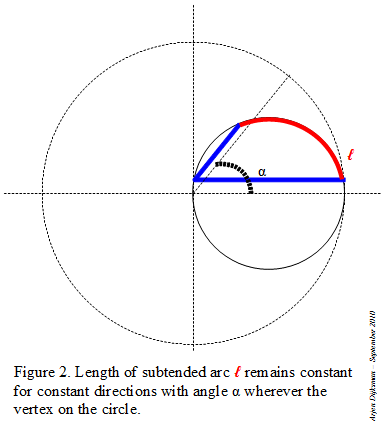
Step 1: I start with a circle in which I inscribe an angle α inferior to 60°. The lines are intercepting an arc on the circle.
Step 2: I duplicate the angle by tracing a little circle centered at one of the endpoints of the arc and with radius the chord of that arc. I repeat the same operation to triplicate the angle (see Figure 1).
Step 3: When two circles of equal size and common radius intersect, two equilateral triangles appear, so I draw both of them: Figure 2.
Step 4: I draw supplementary equilateral triangles at both sides, with the help of the intersections of the circles and the outer lines of the triplicate angle, see Figure 3.
Step 5: The magenta colored equilateral triangle is the Morley triangle of the arbitrary triangle we are looking for. The Morley triangle is a pivotal triangle, so the other vertices of the arbitrary triangle can be found through symmetric construction of the initial inscribing circle centered towards the other sides of the Morley triangle, see the red circles at Figure 4.
Step 6: I complete the figure with the triplicated angles β and γ in the red inscribing circles. The sides of the searched triangle are the outer lines of the triplicated angles, see Figure 5.
With this tripling angle construction, we always obtain an equilateral triangle at the intersection of the trisectors of a triangle. When the initial vertex is moved on the initial inscribing circle, all triangle shapes can be generated for any initial angle α between 0 and 60°, which proves the Morley theorem for any triangle.